|
|
Robert has four jobs his mother expects him to do each day. The jobs
are:
- put dirty clothes away
- make bed
- put dirty
dishes in dishwasher
- put game
system and controllers away
Each day, Robert randomly picks which order he will do the
jobs.
What is the probability that Robert will put the dirty dishes away
after making his bed?
The steps to
this problem, using an organized list, are shown below.
Match each step
with the correct step from the Problem Solving Plan.
Organized Table:
Job 1 | Job
2 | Job 3 | Job 4 | A | B | C | D | A | B | D | C | A | C | B | D | A | C | D | B | A | D | B | C | A | D | C | B | B | A | C | D | B | A | D | C | B | C | A | D | B | C | D | A | B | D | A | C | B | D | C | A | C | A | B | D | C | A | D | B | C | B | A | D | C | B | D | A | C | D | A | B | C | D | B | A | D | A | B | C | D | A | C | B | D | B | A | C | D | B | C | A | D | C | A | B | D | C | B | A | | | | |
a. | I’m sure
that I covered all possible combinations because of how I completed the
table.
| b. | Make an organized list of all possible outcomes, which would be
the different orders that Robert can do the jobs.
| c. | Once the table
is completed, I see that there are a total of 24 different orders for the 4 jobs. Out of the 24
ways, there are 6 times when Job C comes directly after Job B. Therefore the probability of Job C
coming after Job B is 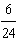 or or 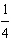 . . | d. | There are four jobs which I will label A, B, C, and
D
Robert randomly picks which order he does the jobs.
I need to
determine the probability that Robert does Job B, THEN Job C. | | |
|